Зачем Maxima школьнику и студенту? или «Задача о невесомом медведе»

В данном посте я хочу убить сразу нескольких зайцев.
Во-первых, еще раз рассказать людям о свободной системе компьютерной алгебры Maxima.
Во-вторых, найти вес «мистического зайца» из несложной задачки для школьников

Таким образом прочитав, данную статью, вы узнаете, что такое Maxima, для каких целей её можно использовать, и как решить систему линейных уравнений в Maxima,

Часть первая: Зачем же студенту или школьнику Maxima?

За все периоды моего обучения на этапах школьного, средне-специального или высшего образования.
Ни один из преподавателей не рассказывал о свободных прикладных математических программах способных упростить жизнь студенту технической специальности.

Почему то в сознании преподавателей лучшим средством для автоматических вычислений являлся Microsoft Excel. Как в колледже, так и в ВУЗе вычисления нам предлагалось делать либо на калькуляторе, либо в Excel. При том, что и колледж, и университет у меня были весьма приличными в своей среде.

Помню чувство эйфории когда я случайно по воле друга познакомился с Matlab.

Мне просто открылся новый мир доступной математики. Теперь я поделюсь им с вами.

Зачем же нам вообще нужны системы компьютерной алгебры?
По моим личным наблюдениям ну и например из данной статьи
Математика может приносить физические страдания,
таким образом, как ни печально это признавать, но среднестатистический молодой человек вполне
может впасть в ступор при виде чего-то сложнее, чем 2*2.

Начну с краткого обзора Maxima.

Как уже говорилось ранее Maxima — свободная система компьютерной алгебры.
Максима обладает широким математическим инструментарием.
От простой арифметики, до символьных или числовых вычислений из области высшей математики (дифференциальные уравнения, интегралы, преобразования Лапласа, ряды Тейлора и так далее. )
Естественно Maxima так же умеет строить графики.

В отличии от более маститых требовательных и весомых Matlab и MathCad.
Максима не требовательна к ресурсам, а самое главное совершенно бесплатна.

Безусловно оговоренные выше программы выполняют широчайший спектр задач,
я думаю не существует программы которая в одиночку могла бы заменить все функции предлагаемых полным пакетом того же Matlab (c включенным модулем символьных вычислений), но мы сейчас будем говорить о простейших вычислениях, которые могут пригодиться студенту.

К тому же Maxima скорее более уместно будет сравнить с Maple. Интернет утверждает, что Maxima – OpenSource аналог Maple (Может быть и действительно так, но сам я не берусь сказать, потому что Maple в чистом виде не видел)

Скачать Maxima и некоторую документацию к ней можно на maxima.sourceforge.net/ru
Естественно есть версия как для Windows, так и для Linux систем.

Максима – программа консольная, но к ней есть различные графические интерфейсы. Пожалуй самый распространенный из них WxMaxima.

Максима написана на языке Common Lisp. Людям знакомым с данным языком, будет несложно ее освоить (а может быть даже и посмотреть как работают функции программы). В прочем у людей вообще не знающих программирования освоение основ Maxima тоже не вызовет больших трудностей.

Чтобы не быть голословным приведу простой пример

введем в Maxima следующее выражение

и как ответ получим

первую производную 3*x^2.

Всё. Ненавистную таблицу производных (у вас наверняка такая была) — можно больше не учить! То же справедливо и для интегралов: введем integrate(cos(x),x); получим: sin(x).

выглядеть будет вот так:

Как это сделать:

Предположим у вас горят руки вы только что поставили максима и хотите увидеть хоть какой то результат:

для того чтобы вычислить допустим производную, откройте WxMaxima
Нажмите на пустое белое пространство левой кнопкой мыши, и скопируйте или вбейте туда эту формулу diff(x^3,x,1); после чего нажмите Control+Enter и вы получите вычисления для данной ячейки. Следует учесть что в Maxima ячейки зависят друг от друга, так например если вы вбили

И посчитаете нажав control+Enter только во второй ячейке
то в ответ получите
(%o2) x+3;

потому что значение посчитанное в предыдущей ячейке программе пока не известно.

Также если вы поменяете значение в ячейке (%i1) x:2; например на (%i1) x:4; не забудьте пересчитать ячейку.

Хотя безусловно вы можете нажав ctrl+R пересчитать сразу все ячейки.

И последний совет: Иногда бывает полезно обнулить процесс вашей бурной деятельности в Maxima, выбрав команду Maxima-> restart maxima

И так я немного рассказал вам о Maxima и готов перейти ко второй части Статьи.

Часть вторая: Решение системы линейных уравнений в Maxima (задача о невесомом медведе)

Как-то пасмурным осенним днем, мой коллега Drzugrik гулял по просторам сети интернет и набрел на данную ссылку: nnm.ru/blogs/samovar1/pedagogi-rezvyatsya

Вытерев, слезы радости и умиления мы всем офисом дружно взялись решать одну из предложенных в данной статье задач.

Итак вот условие задачи.
Вообще задача была представлена графическим способом, но я на всякий случай опишу ее и текстом тоже:

лиса весит столько же сколько заяц и гиря в пять килограмм взятые вместе
волк весит столько же сколько лиса и гиря в четыре килограмма взятые вместе
заяц и лиса весят столько же сколько волк и гиря в один килограмм взятые вместе
медведь весит столько же сколько заяц лиса и волк вместе взятые.

Картинка с задачей:

Итак получив задачу мы сразу же ринулись ее решать.

Начали с создания систем уравнений, а вот дальше наши пути и главное результаты «немного» разошлись.

Что у нас только не получалось:

и медведи с отрицательной массой

и зайцы Мутанты, весящие в три раза больше чем волк

Коллега даже отправил данную задачу своей подруге — педагогу младших классов, но и она потерпела фиаско.

В итоге нашелся среди нас человек способный решить эту задачу.
Но из-за того что смог сделать это он один, осадок остался и дабы развеять свои сомнения, я решил призвать на помощь —ЭВМ.

Я предлагаю вам для начала попробовать найти ответ задачки в ручную, а уже потом заглянуть под спойлер

Для решения задачи в Maxima был введен следующий код:

(%i1) eq1:lisa=zay+5; eq2:lisa+4=volk; eq3:lisa+zay=volk+1; eq4:medved=volk+lisa+zay;
(%o1) lisa=zay+5
(%o2) lisa+4=volk
(%o3) zay+lisa=volk+1
(%o4) medved=zay+volk+lisa

это ввод нашей системы уравнений затем вторая строка

(%i2) solve([eq1,eq2,eq3,eq4],[zay,lisa,volk,medved]);
(%o5) [ [zay=5,lisa=10,volk=14,medved=29] ]

это непосредственно решение уравнений

и третья строка

это проверка решения методом подстановки

Все достаточно просто.

Итак если вы не заглядывали под спойлер, посчитали решение и хотите его проверить, то вам даже не придется устанавливать себе на компьютер Maxima. Вы можете воспользоваться
WEB-интерфейсом по адресу maxima-online.org.

Из недостатков Maxima, пожалуй можно выделить на мой взгляд не очень сильное сообщество.
Например ответ на свой вопрос по обратному преобразованию Лапласа, я так на просторах интернета и не нашел.

P.s Я понимаю что на самом деле, многие читатели Хабра, наверняка хорошо владеют математикой, поэтому вы можете не согласиться со мной, что люди в общем и целом плохо знают математику и даже удивиться как мы смогли найти затруднения в такой простой задачке, но все — относительно. Окружающие меня люди (да и я сам) владеем «царицей наук» весьма слабо, а главное допускаем чисто человеческие ошибки по невнимательности. Поэтому надеюсь, что данная статья поможет людям справиться хотя бы с давно забытыми азами математики.

upd: подправил грамматические ошибки спасибо vasilisc kiselev_dv

• Open source
• Математика

Maxima

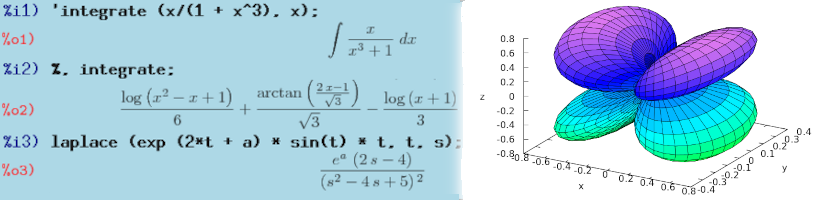
Maxima — система для работы с символьными и численными выражениями, включающая дифференцирование, интегрирование, разложение в ряд, преобразование Лапласа, обыкновенные дифференциальные уравнения, системы линейных уравнений, многочлены, множества, списки, векторы, матрицы и тензоры. Maxima производит численные расчеты высокой точности, используя точные дроби, целые числа и числа с плавающей точкой произвольной точности. Система позволяет строить графики функций и статистических данных в двух и трех измерениях.

Исходный код Maxima может компилироваться на многих системах, включая Windows, Linux и MacOS X. На SourceForge доступны исходные коды и исполняемые файлы для Windows и Linux.

История

Maxima — потомок Macsyma, легендарой системы компьютерной алгебры, разработанной в начале 60-х в Massachusetts Institute of Technology (MIT). Это единственная основанная на Macsyma система, все еще публично доступная и имеющая активное сообщество пользователей благодаря своей открытости. Macsyma произвела в свое время переворот в компьютерной алгебре и оказала влияние на многие другие системы, в числе которых Maple и Mathematica.

Работу над Maxima вел Уильям Шелтер с 1982 года и до своей кончины в 2001 году. В 1998 году он получил разрешение на публикацию исходного кода под лицензией GPL. Выживание Maxima стало возможным только благодаря его усилиям и способностям, мы очень благодарны ему за уделенные проекту время и знания эксперта, которые поддерживали код DOE Macsyma актуальным и качественным. После его кончины была сформирована группа пользователей и разработчиков, ставящая своей целью донести Maxima до широкой аудитории.

Мы постоянно обновляем Maxima, чтобы исправлять ошибки и улучшать код и документацию. От сообщества пользователей Maxima приветствуются замечания и участие в разработке. Большая часть обсуждений проходит в списках рассылки.

• Загрузка
• Документация
• Maxima Project
• Списки рассылки
• Ответы на часто задаваемые вопросы
• Компьютерная алгебра
• Ссылки по Lisp
• Дополнительные пакеты
• Связанные проекты

Программирование в Maxima

Maxima — свободная система компьютерный алгебры (Computer algebra system — CAS), основанная на Common Lisp. В своих функциональных возможностях она едва уступает другим современным платным CAS, таким как Mathcad, Mathematica, Maple; может проводить аналитические (символьные) вычисления, численные расчеты, строить графики (при помощи gnuplot). Имеется возможность написания скриптов и даже трансляции их в код на Common Lisp с последующей компиляцией. В виду того, что maxima писалась из разрабатывалась программистами lisp, ее синтаксис может показаться несколько запутанным, поскольку язык является сразу и императивным и функциональным. Я попытаюсь разъяснить именно эти моменты и доступно изложить суть функционального подхода, и совсем не буду акцентировать внимания на конкретных математических функциях: их довольно легко освоить самостоятельно. В данной статье рассматривается именно особенности исчисления и синтаксических конструкций maxima.

Оболочки

Разумеется, вызывать интерпретатор maxima из консоли не очень удобно. Мы хотим смотреть на красивые формулы, которые отрендерены с помощью latex. Поэтому, для начинающих, я бы посоветовал поставить оболочку wxMaxima. Если вы увлекаетесь TeXmacs — можете настроить и его в качестве оболочки (если честно, я не пробовал). Ну и для любителей emacs есть imaxima, для работы в буфере. Ставится он буквально из коробки.

Знакомство

На первый взгляд все просто: вводим выражение, заканчивающееся точкой с запятой, получаем ответ. Можете испробовать maxima в качестве калькулятора, вычислить сумму двух чисел, подсчитать синус угла и т.п. Копнем глубже, что же происходит.

Атомы

Символы, числа и логические константы true и false представляют собой простейшие объекты системы. Из них выстраиваются все остальные выражения и структуры языка, поэтому их называют атомарными (неделимыми) или просто атомами.

Переменные

В системе различают свободные и означенные переменные. Означенные переменные — связанные переменные, переменные к которым приписано какое то значение. При интерпретации имя переменной заменяется на ее значение. Задать переменную можно с помощью знака «:». Свободные переменные не связаны не с каким значением и мы можем оперировать с ними абстрактно, например, складывать два символьных выражения.

Контекст вычисления

При вычислении каждой команды формируется ее вычислительный контекст. Он представляет собой совокупность связей между именами переменных и их значениями, а так же некоторые параметры интерпретации. Различают два вычислительных контекста: локальный и глобальный. Глобальный контекст — общий для всех интерпретируемых команд, определяет текущее состояние интерпретатора. Локальный контекст создается на время выполнения одной команды, и действителен только для нее. Наиболее приоритетными являются связи и параметры локального контекста.

Здесь значение переменной a берется из глобального контекста, а для локального устанавливается опция развертывания произведений, т.е. дальше произведения не будут развертываться сами по себе.

Блокировка вычислений

Попробуем сложить две переменные. А теперь поставим перед ними символ одинарной ковычки. Это оператор блокировки вычислений. Если мы поставим его перед именем переменной — в результате получим имя этой переменной, перед вызовом функции — символьное выражение вызова функции. Зачем? Иногда вам может потребоваться с помощью одной функции обработать выражение другой функции и на выходе получить функцию или число, например вычисление неопределенного интеграла. Другими словами вы имеете возможность представлять выражение как данные и манипулировать с ним. Однако если вы попробуете остановить вычисление суммы двух чисел, то вычисления не прекратятся. Это связано с тем, что оператор одинарной кавычки не останавливает простейшего упрощения выражения (простые операции над числами, сокращение дробей). Так же вычисления не остановятся, если вы попытаетесь посчитать значение функции рационального (float) аргумента.
И так, система Maxima не различает функции алгоритмические и функции математические, в ней они являются одним языковым элементом. В терминологии самого интерпретатора, операторы которые могут быть вычислены называются verb, те операторы, которые так остаются в невычесленом виде называются noun. Для инициирования вычисления всех noun необходимо в контексте вычислений выставить опцию nouns.

Вычисления

Мы узнали, что интерпретатор различает понятия символьного выражения и его вычисления. В каких случаях происходит вычисление? Самый очевидный случай — когда мы пытаемся посчитать какое то выражение (2+3, например). Ввели выражение — получили его значение. Посчитали функцию от аргумента — получили значение. Ввели имя переменной — получили ее значение. Мы узнали, что значением у переменной может быть как атом, так и символьное выражение. Когда еще происходит вычисление? Вычисление происходит при присваивание переменной значения. Значение стоящее справа от двоеточия вычисляется перед присвоением, поэтому при присвоении переменной символьного выражения мы ставим кавычку, что бы остановить это вычисление. Есть особенный вид присвоения (оператор два двоеточия), когда вычисляется как выражение справа, так и выражение слева. Так же перед вычислением функции вычисляются все ее аргументы.

Результатом вычисления переменной a слева оказывается переменная b.

Пример

Рассмотрим простой пример — построение множества всех подмножеств. Как оказалось, Maxima имеет встроенные типы для работы с множествами, а такой функции, увы, нет. Напишем ее.

Для начала разберемся что есть множества. По видимому, множества в Maxima основаны на другой структуре данных — односвязных списках. Что такое список понимают все. Они имеют три основные функции для работы с ними: получение элемента в голове списка (first), получение списка состоящего из исходного без первого элемента (rest), добавление нового элемента в начало (cons) и объединение двух списков (append). Аналогичные функции имеются и в любой реализации lisp, но чаще всего, называются немного по другому: car, cdr, cons, append соответственно.

Как вы обычно представляли себе алгоритм для решения такой задачи? Можно было бы представить подмножества в виде характеристического вектора и перебрать их все. Однако покажем именно функциональный подход. Нетрудно заметить, что каждый элемент входит ровно в половину подмножеств. Этого простого факта уже достаточно для того, что бы построить рекурсивный алгоритм. Выкинем один элемент a из множества A. Множество всех подмножеств A будет состоять из объединения множества всех подмножеств A\a и множества всех подмножества A\a, где к каждому элементу добавлено a. С помощью последнего утверждения можно сколько угодно рекурсивно понижать размерность задачи, сведя ее к тривиальному случаю. Для реализации нам необходима дополнительная функция от двух параметров (элемента и множества множеств), которая добавляла бы указанный элемент в каждое множество.

Обратим внимание, что объявление функции происходит почти как и в математике. Следует обратить внимание, что при определении правая часть после знака равно не вычисляется. (Для того что бы определить функцию так, что бы ее определение вычислялось необходимо использовать форму define). Здесь появляется новая вычислительная форма if. Она работает так же как и в императивных языках. При выполнении условия вычисляется выражение после then, при невыполнении — после else. Теперь запишем искомую функцию.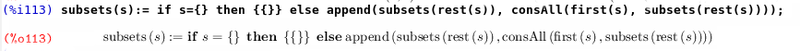

Попробуем что нибудь посчитать.

Конец

Ну вот и все. В следующей статье было бы неплохо описать реализацию наискорейшего градиентного спуска.

• математика
• математическое моделирование
• математический пакет
• функциональное программирование
• lisp
• maple
• mathcad
• matlab
• octave
• mathematica
• maxima
• компьютерная алгебра

При подготовке материала использовались источники:
https://habr.com/ru/articles/158015/
https://maxima.sourceforge.io/ru/
https://habr.com/ru/articles/153853/