Системы компьютерной алгебры

Wolfram Alpha позволяет решать задачи, как аналитическим методом, так и графическим.

Алгоритмы решения задач с помощью WolframAlpha

1. Определить, к какому разделу математики относится задача
2. Выбрать метод решения задачи
3. Составить математическую модель
4. Определить необходимые для решения задачи с помощью Wolfram Alpha функции
5. Ввести формулу и исходные данные
6. Получить результат
7. Провести анализ полученного результата

Особенности, достоинства и недостатки WolframAlpha

Главными достоинствами Wolfram Alpha являются:

1. Наличие бесплатного функционала
2. Возможность работы с любого устройства через браузер.

Главные недостатки Wolfram Alpha:

1. Необходимость постоянного подключения к интернету для работы
2. Наличие платного функционала

Задачи

Задачи из алгебры

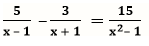
1. Решить уравнение

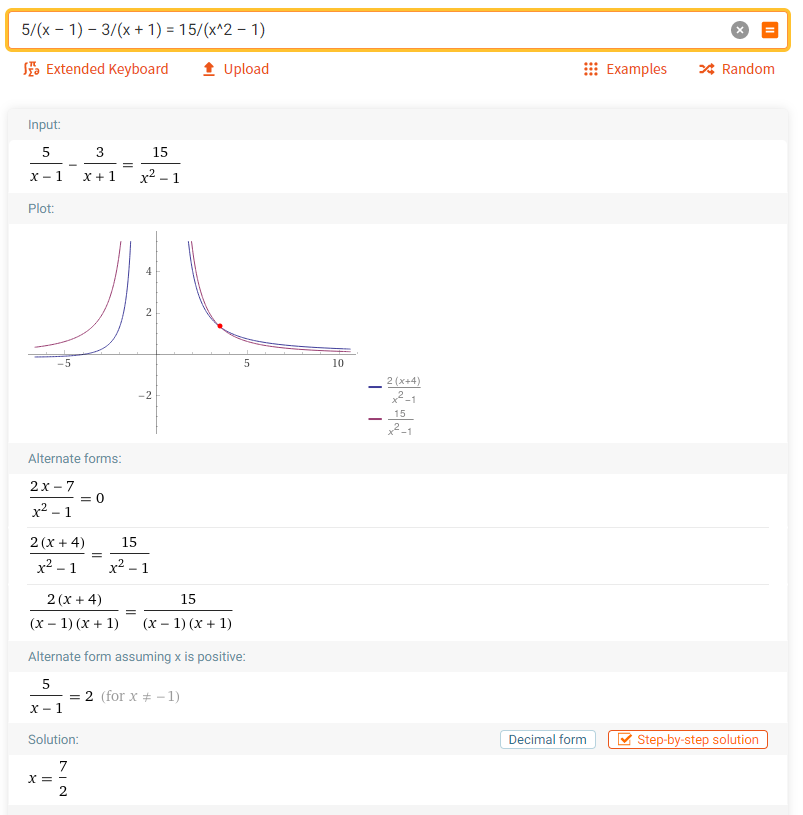
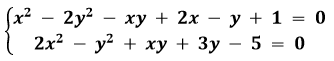
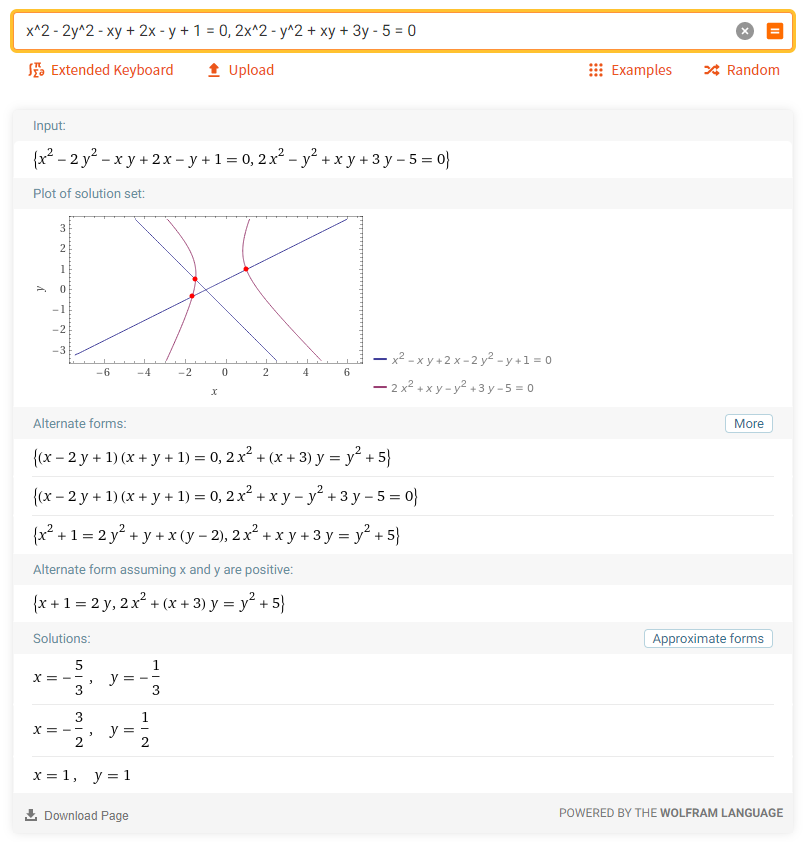
2. Решить систему уравнений:

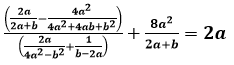
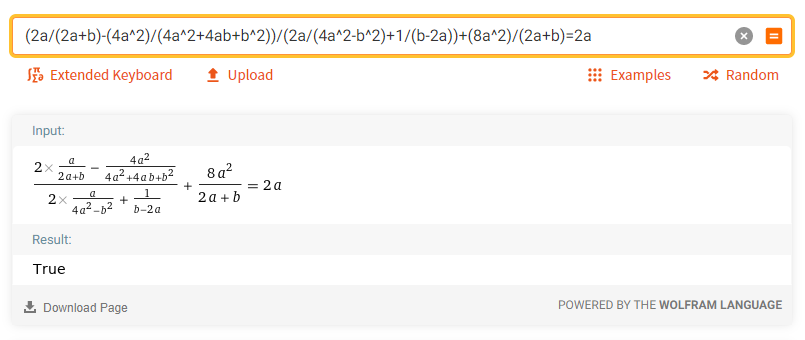
3. Доказать тождество

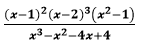
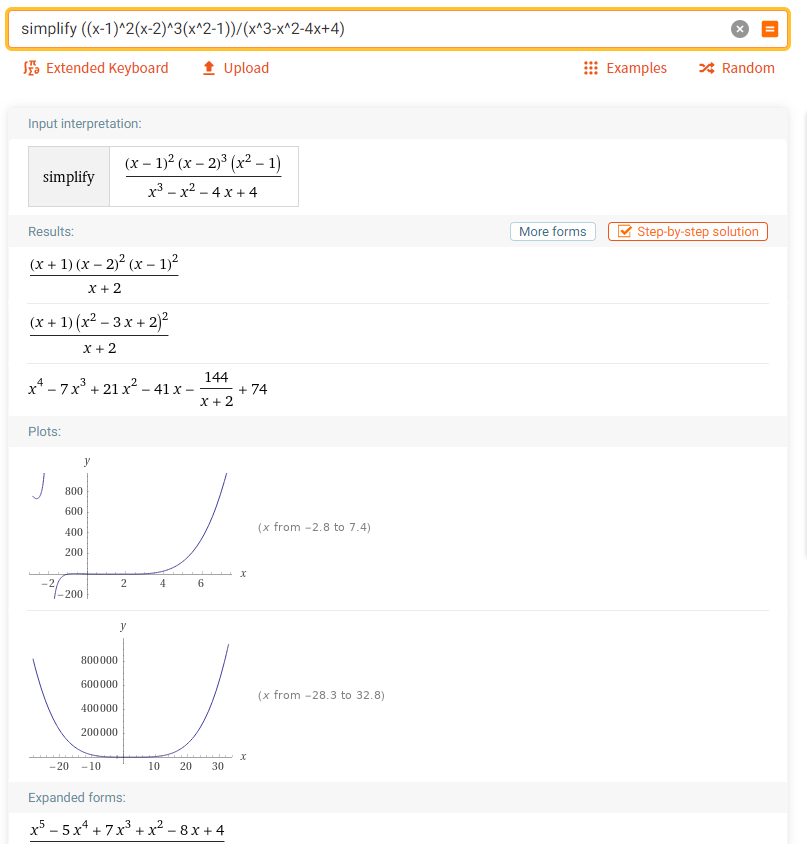
4. Упростить выражение

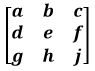
5. Вычислить определитель матицы:

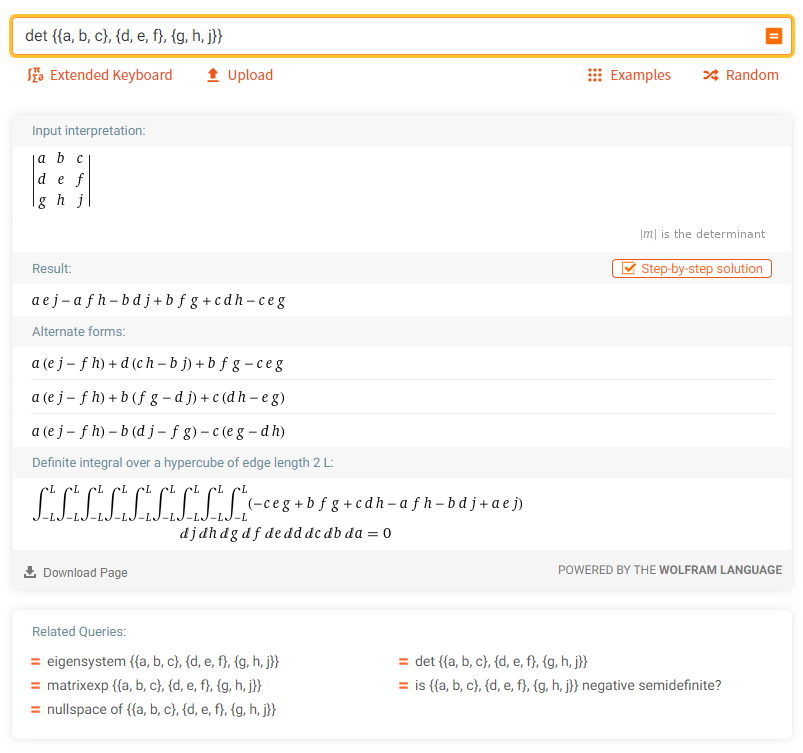
Задачи из математического анализа

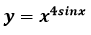
1. Найти производную функции

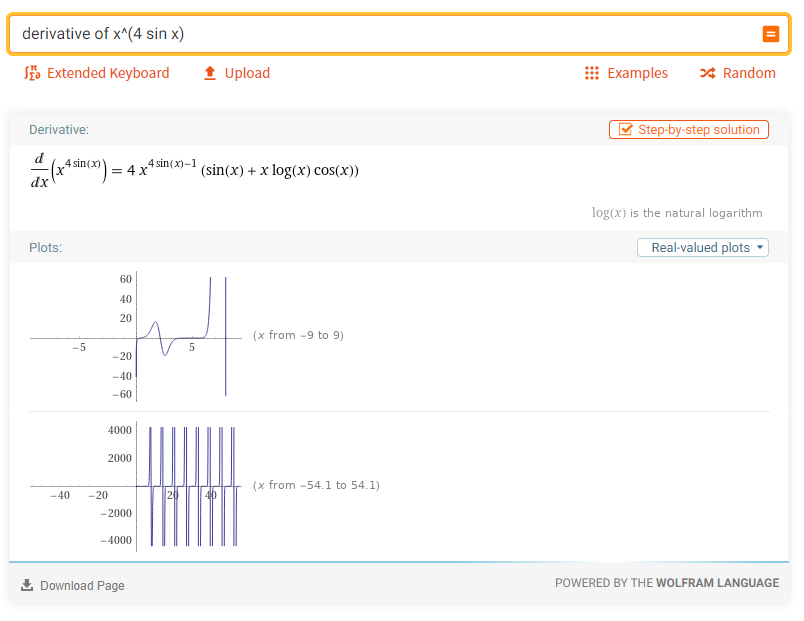
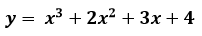
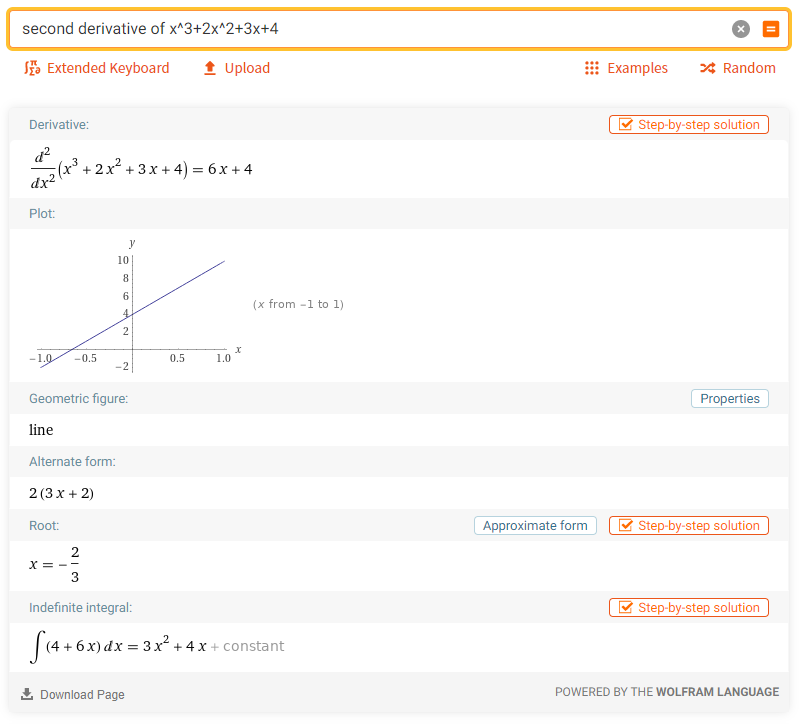
2. Найти производную второго порядка функции

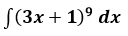
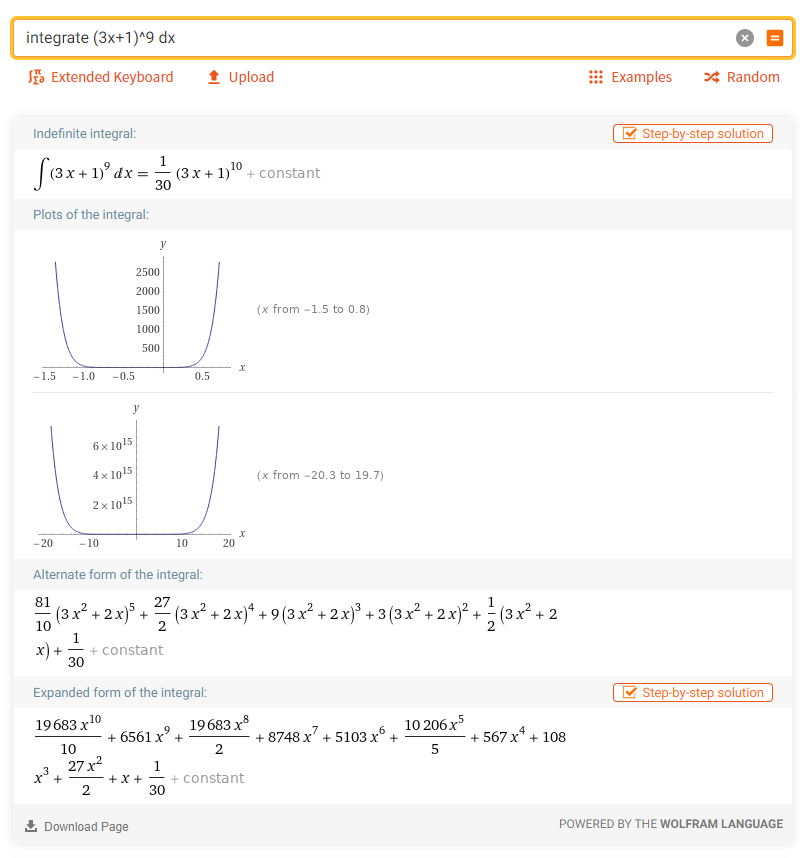
3. Вычислить неопределённый интеграл

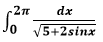
4. Вычислить определённый интеграл

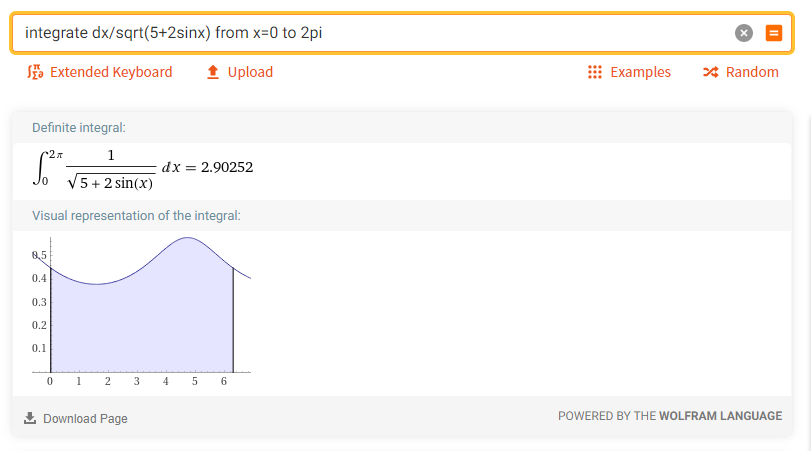
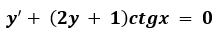
5. Найти корни дифференциального уравнения

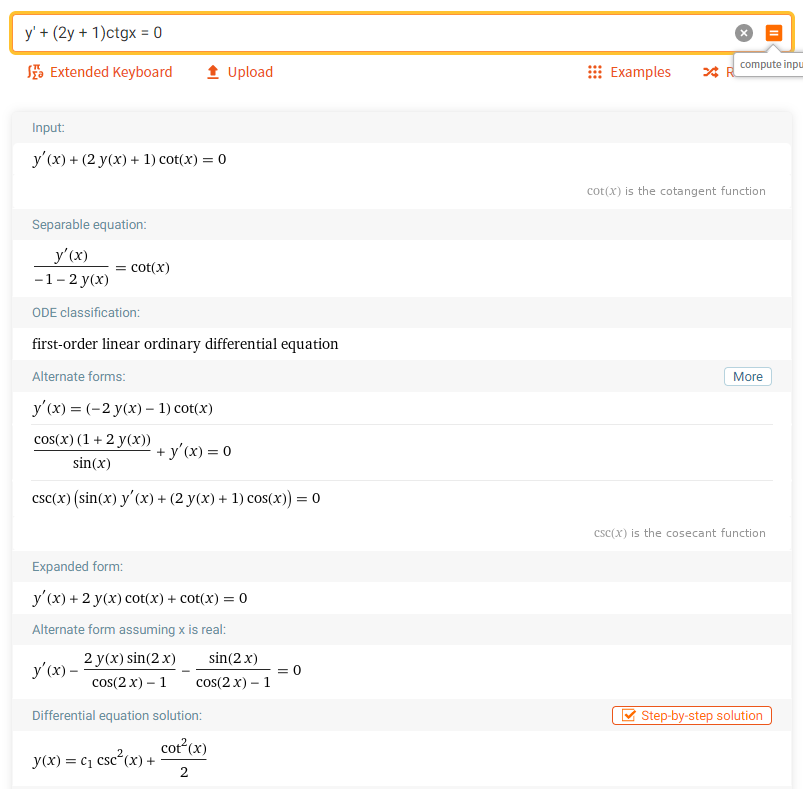
Задачи из геометрии

1. Найти периметр треугольника со сторонами 13, 12 и 5:

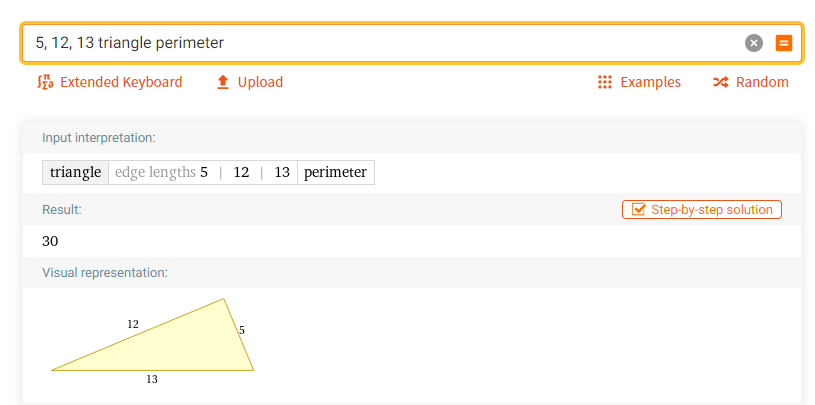
2. Найти пересечение первой прямой, проходящей через точки: (2.85,0.366) и (-0.223,3.89), и второй прямой, проходящей через точки: (0.796,0.215) и (3.256, 5.153):

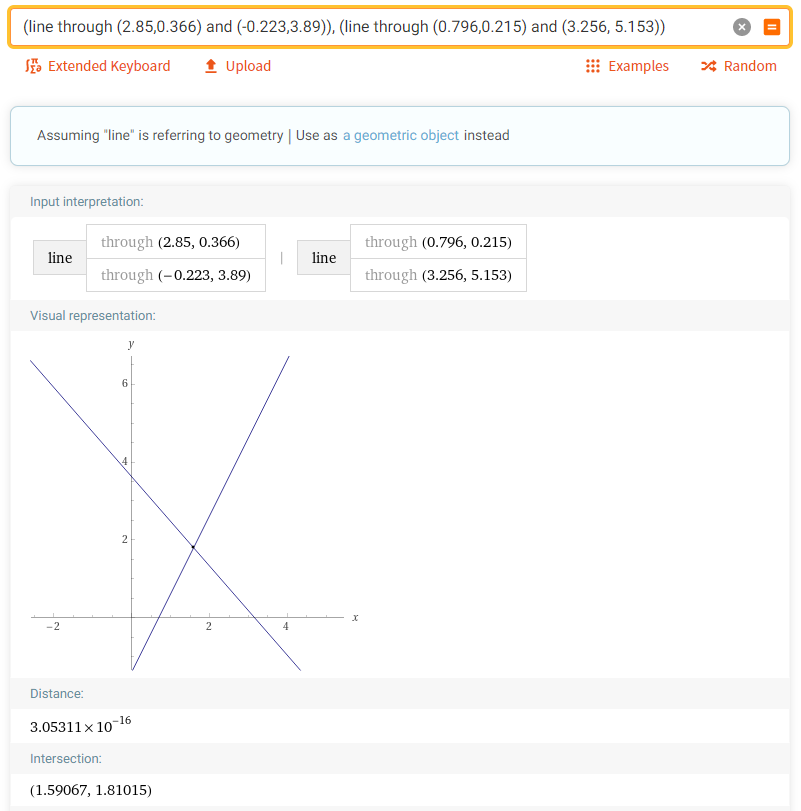
3. Найти площадь четырёхугольника с координатами вершин; (1, -1), (5, 0), (6, 2), (-4, 4):

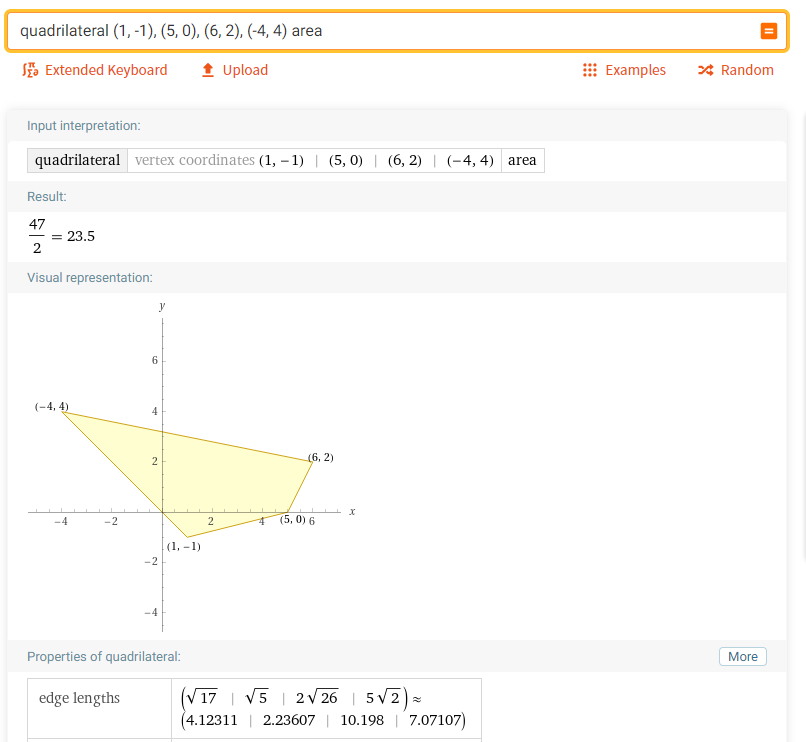
4. Определить углы и радиус вписанной окружности треугольника с вершинами (-4, 3), (5, 7) и (2, -3):

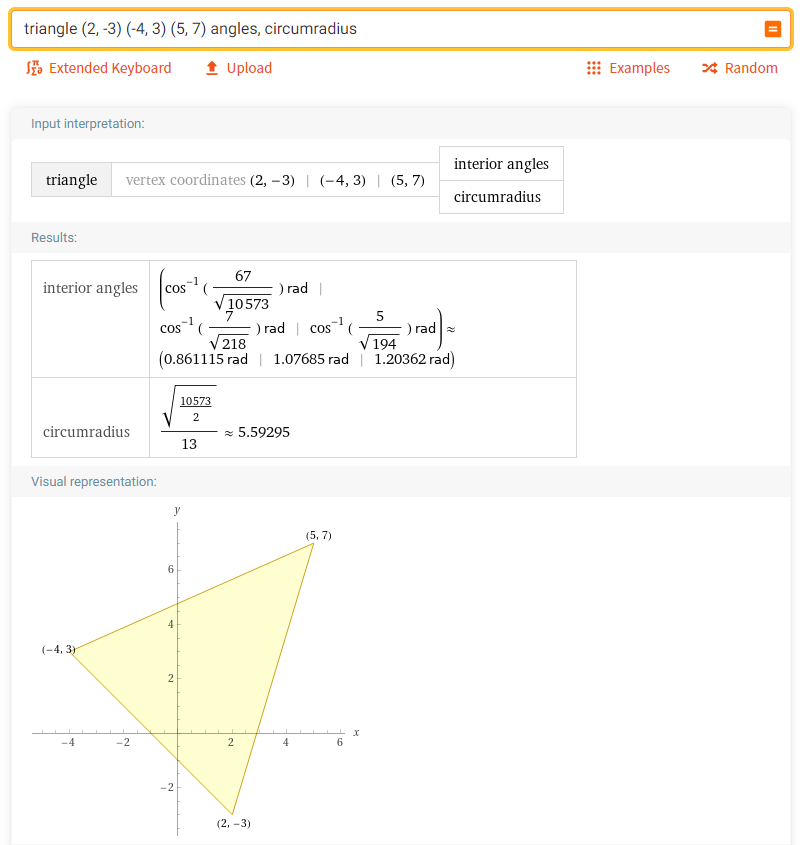
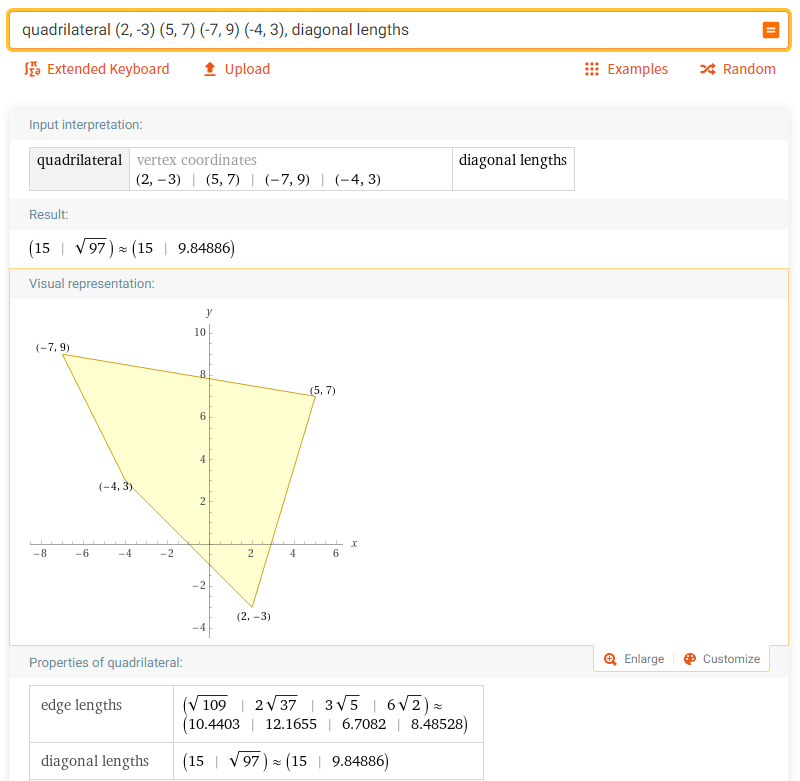
5. Найти диагонали четырёхугольника с вершинами в точках (2, -3) (5, 7) (-7, 9) (-4, 3):

© Группа студентов 2ИВТ(2)/19

Wolfram Mathematica

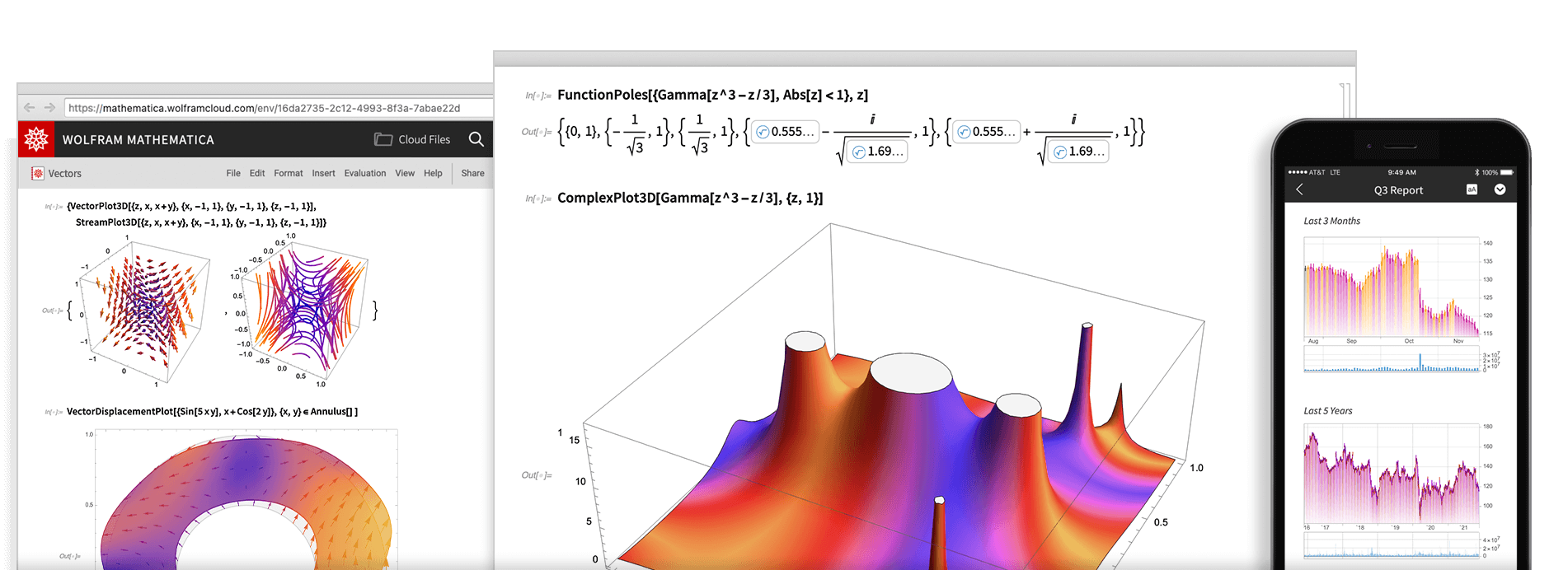
Доступно для рабочего стола,
облака и мобильных устройств

Mathematica

На протяжении трёх десятилетий Mathematica определяет передовой край технических вычислений и обеспечивает основную среду для проведения расчётов для миллионов новаторов, педагогов, студентов и других пользователей по всему миру.

Широко признанная за технические возможности и элегантную простоту использования, система Mathematica обеспечивает цельную интегрированную и постоянно расширяющуюся систему, охватывающую весь спектр технических вычислений, а также доступна бесперебойно в облаке через любой веб-браузер наряду со всеми родными современными системами для рабочего стола.

Нет лучшего выбора для современных технических вычислений

Благодаря энергичному развитию и стабильному видению на протяжении трёх десятилетий, Mathematica не имеет себе равных в большом диапазоне измерений и уникальна в своей поддержке современной среды и организации рабочего процесса для технических расчётов.

Огромная система, тесная интеграция

Mathematica имеет в наличии более 6000 встроенных функций, покрывающих все области технических расчётов—все они тщательно интегрированны для идеальной совместной работы, и все они включены в полностью интегрированную систему Mathematica.

За пределами чисел и математики

Основываясь на трех десятилетиях развития, Mathematica превосходит во всех областях технических расчётов, включая нейронные сети, машинное обучение, обработку изображений, геометрию, науку о данных, визуализацию и многое другое.

Удивительная алгоритмическая производительность

Mathematica строится на беспрецендентно мощных алгоритмах всех предметных областей; многие из них были созданы компанией Wolfram, используя уникальные методы развития и уникальные возможности языка Wolfram Language.

Более высокий уровень, чем когда-либо прежде

Суперфункции, мета-алгоритмы. Mathematica предоставляет прогрессивную высокоуровневую среду с максимальным уровнем автоматизации, что позволяет Вам быть наиболее продуктивными.

Вся функциональность промышленного класса

Mathematica построена с целью предоставления возможностей промышленной мощности, с крепкими эффективными алгоритмами во всех областях, способными решать крупномасштабные задачи с параллелизмом, вычислениями на графических процессорах и многим другим.

Убедительная простота в использовании

Mathematica использует свои алгоритмические возможности и тщательное проектирование языка Wolfram Language для создания уникальной в использовании системы, имеющей предиктивные рекомендации, поддержку ввода на естественном языке и многое другое.

Не только пишите код, но и документируйте

Mathematica использует Wolfram Notebook Interface, который позволяет организовать всё, что Вы делаете, в богатый содержанием документ, который включает текст, выполнимый код, динамичную графику, пользовательский интерфейс и многое другое.

Понятный код

Благодаря когерентному дизайну и использованию интуитивных названий функций, состоящих из полных английских слов, язык Wolfram Language исключительно просто читать, использовать и изучать.

Представляйте свои результаты наилучшим способом

Благодаря утончённой вычислительной эстетике и отмеченному наградами дизайну, система Mathematica представляет Ваши результаты в привлекательном виде, мгновенно создавая передовые интерактивные визуализации и готовые к публикации документы.

Реальные данные напрямую

Mathematica имеет доступ к обширной базе знаний Wolfram Knowledgebase, которая включает актуальные реальные данные из тысяч предметных областей.

Эффективная облачная интеграция

Mathematica теперь эффективно интегрированна с облаком позволяя совместное использование, облачные расчёты и многое другое в уникальной и мощной гибридной среде облака/рабочего стола.

Совместимо с чем угодно

Mathematica построена так, чтобы быть подключенной ко всему: файловым форматам (более 180), другим языкам, Wolfram Data Drop, API, базам данных, программам, интернету вещей, устройствам и даже распределённым копиям самой себя.

Более 150 000 примеров

Начните с практически любого проекта с помощью более 150 000 примеров из Documentation Center, и более 10 000 демонстраций с открытым кодом в Wolfram Demonstrations Project и множества других ресурсов.

Функциональное покрытие

Mathematica основывается на инновационном языке Wolfram Language.

Введение в Wolfram Mathematica

На хабре уже не раз упоминалась Mathematica и если вам хочется начать работать с ней, то эта статья для вас. Я расскажу об основных аспектах работы с нею и покажу несколько интересных нововведений из последних версий Wolfram Mathematica.

Wolfram Mathematica — это программное обеспечение, не только для математических вычислений, это гораздо больше: от моделирования и симуляции, визуализации, документации, до создания веб-сайтов. Mathematica обладает возможностью осуществлять вызовы функций и принимать вызовы с C, .NET, Java и других языков, генерировать C код, компилировать автономные библиотеки и исполняемые файлы.
Обо всех достоинствах Mathematica можно почитать на официальном сайте

Для начала работы с Mathematica вам необходимо её получить и установить на свой компьютер. Mathematica прекрасно работает на Windows, Mac, Linux.
Скачать и бесплатно попробовать Mathematica так же можно на оф. сайте.
Если же вы надумаете её купить, то цены на неё вполне приемлемые. Например для студента за семестровый вариант она обойдётся в $44.95. Для домашнего использования в $295. Если вы планируете использовать её для коммерческих целей, то наилучший вариант лицензии это Standard Edition (Вы получаете подписку на Premier Service и бесплатные обновления).

Изучение

Самая лучшая книга по Mathematica — это встроенный Help. Имеет огромную кучу туториалов и советов. Огромное множество примеров. Всё что вам может понадобится находится там. Это первое место где нужно искать нужную информацию. Однако, если вам нужно больше, в интернете огромное множество сообществ посвещённых Mathematica. (Например: mathematica.stackexchange.com).

Блокноты и Ячейки

• Ячейки ввода – в них задаются команды, которые будут вычислены
• Ячейки результата – в них выводится результат вычислений
• Другие ячейки – ячейки с текстом, заголовки и все остальное

Нумерация ячеек идёт в том порядке в котором вы их запустили. Для того что-бы вычислить значение ячейки нажмите SHIFT+ENTER или правый ENTER, либо Evaluation -> Evaluate Cells.

Для того что-бы обратиться к значению последней вычисленной ячейке используйте знак %.

Бесконечная точность

Одной из замечательных особенностью Mathematica является концепция бесконечной точности. Если результатом вычислений является корень из двух, то она так и напишет.

Вы можете попросить округлить ответ так:

Или же добавить дробную часть (или просто точку) к числам в выражении:

Ввод формул

В Mathematica реализован удобный ввод формул. Но для начала вам могут пригодится палитры (На картинке справа находится Palettes -> Basic Math Assistant).

У каждой кнопочки на палитре, есть свой горячие клавиши. Например, что бы написать знак интеграла нужно нажать Esc int Esc.

Вот список наиболее часто используемых горячих клавиш:

• CTRL+2 – Шаблон квадратного корня
• CTRL+6 – Верхний индекс
• CTRL+7 – Надстрочный символ
• CTRL+- – Нижний индекс
• CTRL+= – Подстрочный символ
• CTRL+/ – Дробь
• CTRL+2, затем CTRL+5 – Корень любой степени
• ALT+ENTER – Создает новую ячейку
• SHIFT+CTRL+D – Разбивает текущую ячейку
• SHIFT+CTRL+M – Склеивает несколько ячеек

Выражения, Списки, Функции

Все что записано внутри ячеек является выражениями. Каждое выражение состоит из головы и списка. Например в выражение Power[2, 2]. В нём головой является Power, а списком 2, 2.
Даже 2+2 является выражением. Чтобы посмотреть как Mathematica интерпретирует ввод, есть функция FullForm:

Функция Hold просит математику не вычислять выражение. Обратной функция является Evaluate.

Списки в Mathematica создаются при помощи фигурных скобок: <. >, что является сокращением от List[. ].

Для манипуляции со списками в Mathematica есть огромная куча функций. Всё что вам может когда-нибудь понадобиться уже есть там. Вам остаётся только найти нужную функцию.

Для того чтобы получить элемент списка есть функция Part, c сокращённым вариантом в виде двойных квадратных скобок [[. ]] либо с толстыми скобками (Esc [[ Esc).

Поскольку всё является выражениями (и списки тоже), мы может получить голову выражения таким вот способом:

Таким образом индекс первого элемента в списке это 1.

Так же есть возможность заменить голову любого выражения. Это делает функция Apply[head, expression]. Либо её сокращённый вариант @@.

В Mathematica есть несколько способов применить функции(головы) к выражениям. Это обычные квадратные скобки: f[x], префикс: f@x, постфикс: x // f

А так же инфикс: из x ~ f ~ y получим f[x, y].

Однострочное программирование

В Mathematica есть множество функций для обычного программирования, такие как For, If, Switch. Однако, их лучше не использовать без крайней необходимости. Так как практически всё тоже самое можно сделать в одну строчку при помощи специальных функций и их комбинированием (поначалу бывает сложно перестроиться на такой стиль программирования).

Вот хорошее видео демонстрирующее как работают некоторые из функций:

Динамические интерактивные вычисления

Одной из замечательнейших возможностью Mathematica, являются динамические вычисления. Они позволяют манипулировать данными и смотреть на то как динамически меняется результат.

Для динамических вычислений используются функции Dynamic, Manipulate и др.

Заключение

В статье я рассказал о основных аспектах работы в Mathematica. Есть также несколько других важных моментов, таких как паттерны, модули, ядра. О них я расскажу в следующий раз, если эта тема будет интересна вам.

PS Обо всех найденных ошибках сообщайте мне в личку.

UPDATE
Картинки исчезли. Восстановил пост в своём блоге elfet.ru/introduction-to-wolfram-mathematica

• Программирование
• Математика

При подготовке материала использовались источники:
https://ivt-computer-algebra.github.io/wolfram.html
https://www.wolfram.com/mathematica/index.php.ru?source=footer
https://habr.com/ru/articles/180925/